Bert Simonovich's Design Notes

Originally published Signal Integrity Journal, February 23, 2021

Signal and power integrity (SI/PI) simulations, measurements, and analysis usually live in two different worlds, but occasionally these worlds collide. One such collision occurs when we refer to characteristic impedance, Z₀. Traditionally the PI world lives in the frequency domain while the SI world lives in the time domain.

When designing a power distribution network (PDN) in the PI world, we are mostly interested in engineering a flat impedance below a target impedance from DC to the highest frequency components of the transient current. Practically this is achieved with a network of capacitors with different values connected to the respective power planes as shown in Figure 1.

Figure 1 A simplified model of a typical PDN courtesy [1].

In the real world, there is no such thing as an ideal capacitor. There are always parasitic elements known as equivalent series inductance (ESL) and equivalent series resistance (ESR). Physical characteristics of the PCB, like component mounting inductance, plane spreading inductance, via and BGA ball inductance, along with voltage regulator module (VRM) characteristics also contribute to the impedance profile. When connected together, the interaction of capacitors and parasitic inductance and resistance create a transfer impedance profile with resonant peaks and anti-resonant nulls as shown in Figure 2.

The transfer impedance between the VRM and the load is calculated and plotted in the frequency domain with a log-log scale. The resulted impedance curve is then compared to the target impedance (Z_target), which is estimated based on the allowed noise ripple and maximum transient current. The flat target impedance is frequency independent in the analysis.

Figure 2 Impedance profile of the PDN as viewed from the pads on the die power rail courtesy [1].

Resonant peaks are due to ESL of one capacitor connected in parallel with another capacitor. Anti-resonant nulls are due to the series combination of ESR, ESL, and C for each capacitor. Different capacitor values will have anti-resonant nulls at different frequencies.

But in the PI world, there is a rarely talked about characteristic impedance, Z₀. In this case, it refers to the geometric average of the reactive impedance of a capacitor (XC) and reactive impedance of an inductor (XL).

Equation 1

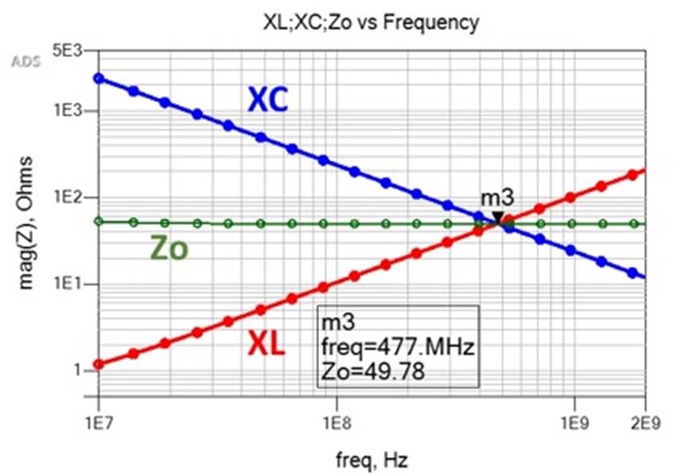
At resonance, XL and XC intersect at the characteristic impedance and are equal as shown in Figure 3.

Figure 3 Inductive and capacitive reactance plot of ideal inductor and capacitor versus frequency. At resonance, XL and XC are equal and intersect at the characteristic impedance, Z₀. Simulated with Pathwave ADS [6].

This is a very important observation, and it is where the SI/PI worlds collide.

In the SI world, characteristic impedance, Z₀ refers to the instantaneous ratio of the voltage to current of a wave front traveling along a uniform transmission line without reflections. For an infinitely long uniform transmission line, Z₀ equals the input impedance.

The characteristic impedance of a lossy transmission line is defined as:

Equation 2

Where R is resistance per unit length; G is conductance per unit length; L is inductance per unit length; and C is capacitance per unit length. For a lossless uniform transmission line, R and G are assumed to be zero and thus the characteristic impedance is reduced to:

Equation 3

Time Domain Reflectometer

In the SI world, we usually use a time domain reflectometer (TDR) to measure characteristic impedance, but more often than not, the measured impedance we get is not what we predicted with a 2D field solver. Many 2D field solvers used by most PCB FAB shops only calculate the lossless characteristic impedance of the cross-sectional geometry at a single frequency, defined by the dielectric constant (D_k). It has no input for conductor resistivity, dielectric loss, or how long the conductor(s) is.

So the issue is: we design the stackup, then do our SI modeling analysis based on stackup parameters and matching characteristic impedance. But the PCB FAB shop will often adjust the line width(s), over and above normal process variation, so that when measured, the impedance will fall within the specified tolerance, usually +/-10 percent.  

Part of the problem lies with the method used to take the measurements. Most PCB FAB shops follow IPC-TM-650 Test Methods Manual [2]. But it has limitations because Z₀ measured is derived and cannot be directly measured. The reason is the measurements include resistive and dielectric losses, up to the point where the measurement takes place along the TDR plot.

Resistive loss often results in a slow monotonic rise in the impedance profile, shown in the example TDR plot of Figure 4. IPC-TM-650 specifies a measurement zone between 30-70 percent to avoid probing induced ringing affecting the measurements. Most PCB FAB shops will measure an average impedance over this range, usually in the center region.

Depending on the linewidth, thickness and dielectric dissipation factor (D_f), the slope of the monotonic rise will vary.

Figure 4 Example TDR plot showing slow monotonic rise in impedance due to resistive losses and IPC-TM-650 measurement zone.

The problem is that the IPC-TM-650 test method was last updated back in 2004, when higher dielectric loss, along with wider line widths and thicker copper weights, were used more often. A higher D_f tends to compensate for resistive loss by flattening the slope as shown in Figure 5.

On the bottom left is a simulated TDR plot using a high loss dielectric with D_f = 0.024. The right side has the exact same geometry properties except D_f = 0.004. The average impedance, when measured at the 50 percent point, is 49.8 Ohms on the left side vs. 51.4 Ohms on the right side. We also confirm flatter slope for high loss material.

The actual characteristic impedance predicted by a Polar SI9000 2D field solver [5] in Figure 5 is 49 Ohms. For higher loss material, measuring within the measurement zone would pass without any issues. But for lower loss material, the resistive loss dominates and measuring within the measurement zone will give ~5 percent higher impedance reading compared to the higher loss material. The correct measurement point for Z₀ is, in fact, the initial dip, equivalent to the field solver prediction. Depending on the tolerance specified, this may affect yield and cost.

Figure 5 Characteristic impedance prediction by Polar SI9000 2D field solver [5] (top). Simulated 2 inch TDR plots using a high loss dielectric (bottom left) vs. low loss dielectric with exactly the same geometry (bottm right). A higher Df compensates for higher resistive loss thereby flattening the curve. Simulated with Pathwave ADS [6].

Today, with the push to low loss dielectric and finer line widths with thinner copper weights, measuring the true transmission line characteristic impedance using a TDR becomes more challenging. This is even more so when measuring differential impedance, because a change in line width space geometry can have a more profound effect on measured differential impedance.

Using the first article build of a new design, as an example, let’s assume the correct characteristic impedance, when measured at the beginning of the slow monotonic rise of a TDR plot, is on the high end of nominal +10 percent tolerance. Let’s say it’s 54 Ohms.  But because of the low loss dielectric and high resistive loss, the TDR measurement at the midpoint is now reading 5% higher at 57 Ohms. This would imply the impedance is now out of spec over nominal and the board would be scrapped.

The PCB fab shop will then go back and adjust the linewidth accordingly for the next build to bring the measurement within range to their measurement set up. Doing this effectively lowers the true nominal characteristic impedance!

If subsequent manufacturing variations pushes the measured impedance within the measurement zone on the low end of the -10 percent tolerance, say 44 Ohms, then the true characteristic impedance, if measured at the initial dip, will be 5 percent lower at 42 Ohms and be out of spec. But the board will pass because it was measured following IPC-TM-650 test method.   

2-port Shunt Measurement

But what if there were another way? What if we could borrow impedance measuring techniques from the PI world to determine the true transmission line characteristic impedance in the SI world?  Well there is. Enter the 2-port shunt measurement technique.

For example, in the PI world, to measure ESL and ESR of a chip capacitor, of a device under test (DUT), a 2-port shunt measurement is often used. It is much like the 4-point Kelvin measurement technique used to measure very low DC resistance.

The 2-port shunt measurement is usually done with a 2-port vector network analyzer (VNA). Port 1 of the VNA sends out a calibrated signal, and port 2 measures the voltage signal across the DUT. Often an isolation transformer is also used to break the inherent ground loop when measuring ultra-low impedances [3].

Once the measurements have been completed and S-parameters saved in touchstone format, further analysis can be done in your favorite SPICE simulator. Figure 6 is a generic schematic using popular Pathwave ADS [5] that can be used for 2-port shunt analysis.

When port 1 and port 2 are connected to port 1 of the DUT and port 2 of the DUT is grounded, the impedance of the DUT can be determined by [3];

Equation 4

Figure 6 Generic Pathwave ADS [6] schematic used for 2-port shunt analysis on a S2P file for DUT.

If we replace the DUT in Figure 6 with a capacitor and inductor, we get an impedance plot shown in Figure 7.  As we saw earlier, when we take the geometric average of the inductive and capacitive reactance using Equation 1, we get the characteristic impedance. If we apply Equation 4 to the results of a 2-port shunt measurements of a capacitor and inductor, we get exactly the same results as shown in the top of Figure 7.

When we replace the capacitor and inductor with a S-parameter file of a transmission line model from Figure 5, we get the plot shown at the bottom of Figure 7. Except for the resonant nulls and peaks, up to a certain frequency, the impedance of a transmission line looks like the impedance of a capacitor when the far-end is open, and looks like the impedance of an inductor when the far-end is shorted. And because of that, this is where the two worlds collide!

If we take the geometric average of the impedance when the far-end is open (Z_open) or shorted (Z_short), we get the characteristic impedance at that frequency. We note where the red and blue impedance lines first intersect, is exactly the geometric average characteristic impedance at that frequency.

Also worth noting, the lines intersect at half of the frequency between the peaks and valleys at higher frequencies as well.

Figure 7 Impedance of inductive and capacitive reactance vs. frequency (top) and impedance of a transmission line vs. frequency (bottom) when the far-end is open (solid red) compared to when the far-end is shorted (solid blue). The intersection of the red and blue lines is exactly the characteristic impedance. Simulated with Pathwave ADS [5].

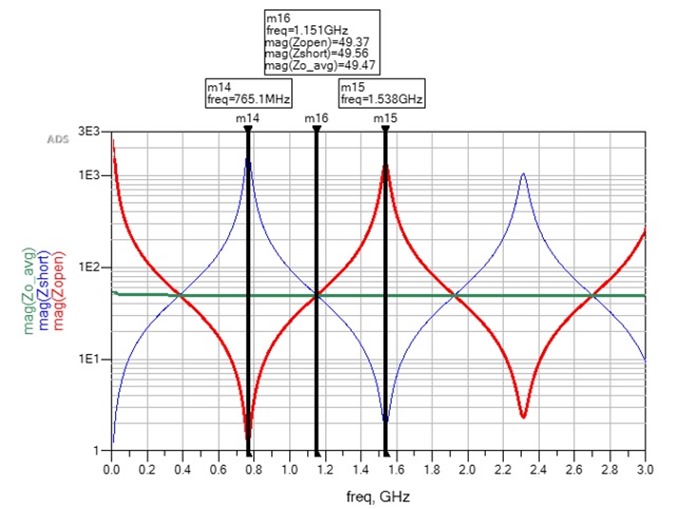
We can see this more clearly if we replot Figure 7 bottom using a linear scale for the x-axis, as shown in Figure 8. This is a very powerful observation. What this means is that when we measure the impedance half way between a peak and adjacent valley, of either the red or blue plot, it is the characteristic impedance of the transmission line at that frequency.

Thus, only an open or shorted end measurement is all that is needed to determine the characteristic impedance. For example, if we look at the red curve alone, then measure the first resonant null (m14) and adjacent peak (m15), the characteristic impedance (mag(Zopen) is measured exactly at one half the frequency between the two (m16). 

Figure 8 Impedance of a transmission line vs. frequency on a linear scale when the far-end is open (solid red) compared to when the far-end is shorted (solid blue). The intersection of the red and blue lines half way between respective peaks and valleys is the characteristic impedance. Simulated with Pathwave ADS [6].

The first resonant red null and blue peak represent the quarter-wave resonant frequency due to open and shorted end. Each respective red null and blue peak following are the odd harmonics of the first quarter-wave resonant frequency.

Knowing this, we can now determine the phase or time delay (TD) of the transmission line as being one quarter of the period of the resonant frequency (f₀).

Equation 5

Because resonant nulls and peaks occur at the resonant frequency, we can also determine the effective dielectric constant (D_keff). Given the speed of light (c) = 11.8 in. per nanosecond, the length of the transmission line (len) in in. and quarter-wave resonant frequency (f₀), D_keff can be determined by:

Equation 6

CMP28 Case Study

Figure 9 Photo of a portion of CMP-28 test platform courtesy of Wildriver Technology [8] used for measurement validation.

To test the accuracy of this method, measured data from a CMP28 test platform, shown in Figure 9, was used for measurement validation. S-parameter (s2p) files from 2 inch and 8 inch single-ended stripline traces were provided as part of CMP-28 design kit courtesy of Wildriver Technologies [8]. The 6-inch transmission line segment S-parameter data was de-embedded courtesy of AtaiTec Corporation [9].

The characteristic impedance, based on trace geometry and stackup parameters, was modeled in Polar SI9000 [5]. Using D_k from data sheet tables @ 10GHz, and correcting for conductor roughness [10], the characteristic impedance predicted was 49.66 Ohms, as shown in Figure 10.

Figure 10 Polar SI9000 field-solver [5] characteristic impedance prediction of CMP28 trace geometry.

Touchstone S-parameter DUT files were connected with far-end open, shorted, and terminated as shown in Figure 11. The TDR plot, with far-end terminated, shows an impedance of 50.57 Ohms, when measured at the initial peak. Then it takes an immediate dip to approximately 50 Ohms before continuing with a slow monotonic rise with some ripples. If the DUT was a uniform trace, with connector discontinuity de-embedded, we would not see the initial peak followed by the dip.  This signature strongly suggests that the DUT is not uniform and thus it is very difficult to determine the actual characteristic impedance using IPC-TM-650 test method alone. 

But only after taking 2-port shunt measurements can we confirm the true characteristic impedance. As shown, Zoavg is 50.68 Ohms where the red and blue curves cross at 122.5 MHz, and confirms the true measurement point in the TDR plot is the initial peak. Both are about 1 Ohm higher compared with 2-D field solver results in Figure 10.

If the length of the transmission line simulated above is 6 in. and f₀ =248.2 MHz, then TD = 1 ns and D_keff = 3.92, using Equation 5 and Equation 6 respectively.

Figure 11 Measured results from a CMP28 test platform design kit, courtesy of Wildriver Technology [8].

But wait a minute. Why is D_keff is higher than what was used in the 2-D field solver in Figure 10?

One reason is due to process variation of the material and fabrication. The actual D_keff is determined by the final thickness of dielectric and the roughness of the copper, which also increases inductance affecting TD [10] [11]. But the main reason is D_k is frequency dependent and the value used in the field solver was at 10 GHz, based on laminate supplier’s D_k/D_f tables.

Since TD, ultimately determines D_keff, it does not represent the intrinsic property of the dielectric material. Because D_keff varies with frequency, it was calculated at the first resonant null of 248.2 MHz, which is at a much lower frequency for D_k than the frequency originally used to select D_k in the field solver.

As can be seen in Figure 12, a simulated vs. measured 2-port shunt frequency plot, with far-end open and shorted, we get exactly the same information, compared to the traditional method used to validate characteristic impedance and D_keff.

If we measure the 39^th odd harmonic frequency (H) at 9.884GHz for the resonant null closest to 10GHz, equating to the value of D_k used in Polar Si9000 2D field solver, D_keff can be calculated with Equation 7:

Equation 7

The bottom right plot of Figure 12, shows D_keff simulated (blue) vs. measured (red). As we can see, the measured D_keff at 248.7 MHz is 3.94; pretty much agreeing with our earlier calculation of 3.92 using Equation 6. Furthermore, when we compare D_keff = 3.76 at 9.884 GHz, it agrees with our calculation for the 39^th harmonic frequency from Equation 7. The reason there is still a slight difference in D_keff is because the added delay due to inductance due to roughness [11] was not factored into the simulated model.

The bottom left is a TDR plot that shows measured impedance (red) vs. simulated (blue) over time. The marker at the beginning of the initial dip (m6) represents the characteristic impedance with highest frequency harmonics included in the incident step edge of TDR waveform. The marker at the end (m16) represents the impedance at twice the TD with high frequency harmonics attenuated due to dispersion of the lossy dielectric and resistance of trace length.

When we measure Zoavg_meas impedance of DUT at 9.884GHz, at the top plot of Figure 12, it agrees pretty well with the simulated and measured TDR plot at the initial step.

Figure 12 Comparison of PI world 2-port shunt measurement results for transmission line characteristic impedance and D_keff compared to traditional SI world measurement results. Top plot is the 2-port shunt simulated vs. DUT impedance measurements at the fundamental and 39^th harmonic frequencies. Bottom left is beginning and end impedance measurements on TDR plot. Bottom right measuring equivalent D_keff at fundamental and 39^th harmonic frequencies.  

Summary and Conclusion

Sometimes, when SI and PI worlds collide, we get the best of both worlds. By borrowing a simple 2-port shunt impedance measuring technique from the PI world, we have another tool at our disposal to measure true characteristic impedance, TD, and effective D_k from a uniformly designed transmission line in the SI world. The advantage is, unlike a TDR measurement, measuring true characteristic impedance using 2-port shunt method is not influenced by resistive or dielectric losses.

References

1. L. Smith, S. Sandler, E. Bogatin, “Target Impedance Is Not Enough,” Signal Integrity Journal, Vol. 1, Issue 1, January 2019; URL: https://www.signalintegrityjournal.com/ext/resources/MEDIA-KIT-2019/January-2019-Print-Issue/SIJ-January-2019-Issue_eBook_-V2.pdf
2. IPC-TM-650 Test methods Manual, Number 2.5.5.7, “Characteristic Impedance of Lines on Printed Boards by TDR”, Rev. A, March, 2004
3. I. Novak, J. Millar, “Frequency-Domain Characterization of Power Distribution Networks,” Artech House, 685 Canton St., Norwood, MA, 02062, 2007.
4. Pathwave Advanced Design System (ADS) [computer software], Version 2021, URL: http://www.keysight.com/en/pc-1297113/advanced-design-system-ads?nid=-34346.0&cc=CA&lc=eng
5. Polar Instruments Si9000e [computer software], Version 2018, URL: https://www.polarinstruments.com/index.html
6. Keysight Pathwave Advanced Design System (ADS) [computer software], Version 2021, URL: http://www.keysight.com/en/pc-1297113/advanced-design-system-ads?cc=US&lc=eng.
7. E. Bogatin, “Bogatin’s Practical Guide to Transmission Line Design and Characterization for Signal Integrity”, Artech House, 685 Canton St., Norwood, MA, 02062, 2020
8. Wild River Technology LLC 8311 SW Charlotte Drive Beaverton, OR 97007. URL: https://wildrivertech.com/
9. AtaiTec Corporation, URL: http://ataitec.com/products/isd/
10. B. Simonovich, “A Practical Method to Model Effective Permittivity and Phase Delay Due to Conductor Surface Roughness“, DesignCon 2017 proceedings, Santa Clara CA.
11. V. Dmitriev-Zdorov, B. Simonovich, I. Kochikov, “A Causal Conductor Roughness Model and its Effect on Transmission Line Characteristics”, DesignCon 2018 proceedings, Santa Clara, CA.
12. I. Novak et al, “Determining PCB Trace Impedance by TDR: Challenges and Possible Solutions”, DesignCon 2013 proceedings, Santa Clara, CA.
13. S. Sandler, “Easy trick to measure plane impedance with VNA”, EDN Asia, 2014, URL: https://archive.ednasia.com/www.ednasia.com/STATIC/PDF/201410/EDNAOL_2014OCT21_TEST_TA_01.pdf%3FSOURCES=DOWNLOAD