Archive for March 2019
Simonovich “Cannonball” Conductor Roughness Model Demystified
Recently on the SI-List there was great debate on whether or not my Cannonball model can be used to determine surface ratio and radius of sphere parameters needed for Huray roughness model from data sheets alone.
The author of this paper, “Conductor surface roughness modeling: From “snowballs” to “cannonballs”, [1] argues it is impossible to accurately model transmission lines from data sheets alone and seems to imply that because I had measured data in advance that I had magically “adjusted” Rz parameter to get such good correlation to measurements in my EDICon 2016 paper, “Practical Model of Conductor Surface Roughness Using Cubic Close-packing of Equal Spheres” [5].
Unfortunately his paper has created more confusion than clarity. To be clear, there is only ONE “Cannonball” model, and it is based on the cubic close packing of equal spheres, also known as face-centered cubic (FCC) packing.
The author of [1] also advocates using a material model identification methodology, similar to what I like to call the Design Feedback Method, shown in Figure 1. The author believes it is the only “accurate” way of determining printed circuit board (PCB) material properties for modeling.
Figure 1 Design Feed Back Method flow chart
This involves designing, building and measuring a test coupon with the intended PCB trace geometry to be used in final design. After modeling and tuning various parameters to best fit measured data, material parameters are extracted and then used in channel modeling software to design the final product.
The problem with this approach for many small companies is: TIME, RESOURCES, and MONEY.
-
Time to define stackup and test structures.
-
Time to actually design a test coupon.
-
Time to procure raw material – can take weeks, depending on scarcity of core/prepreg material.
-
Time to fabricate the bare PCB.
-
Time to assemble and measure.
-
Time to cross-section and measure parameters.
-
Time to model and fit parameters to measurements.
Then there is the issue of resources, which include having the right test equipment and trained personnel to get trusted measurements.
In the end this process ultimately costs more money, and material properties are only accurate for the sample from which they were extracted for the software and roughness model used. There is no guarantee extracted parameters reflect the true material properties.
There will be variation from sample to sample built from the same fab shop and more so from different fab shops because they have a different etch line and oxide alternative process.
For example Figure 2 shows measurements from two boards of the same design. As you can see there are differences in both insertion loss and TDR plots. Which curve do we use to fit parameters for material extraction to use in simulations? How many do we have to build and test to get a statistical sample of reality? How much time will this take? And how much money will it cost, especially if several PCB stackup geometries are required?
Figure 2 Comparison of insertion loss and TDR measurements of two boards of the same design
But, as Eric Bogatin often likes to say, “Sometimes an OK answer NOW is better than a good answer late”. For many signal integrity engineers, and design consultants, like myself, have to come up with an answer sooner, rather than later for many reasons. And depending on the issue at hand, those answers may be good enough. This was the initial motivation for my research.
So where do we get these parameters? Often the only sources are from manufacturers’ data sheets alone. But in most cases, the numbers do not translate directly into parameters needed for the EDA tools.
This paper will revisit the Cannonball model as it applies to the CMP-28 reference platform from Wildriver Technology [14], and as part of it I will show:
-
How to determine effective dielectric constant (Dkeff) due to roughness from data sheets alone.
-
How to apply my simple Cannonball stack model to determine roughness parameters needed for Huray model from data sheets alone.
-
How to apply these parameters using Simbeor software [10].
-
How to pull it all together with a simple case study.
But before we get into it, it is important to give a bit of background on material properties and PCB fabrication process.
Electro-deposited Copper
Electro-deposited (ED) copper is widely used in the PCB industry due to its low cost. A finished sheet of ED foil has a matte side and drum side. The matte side is usually treated with tiny nodules and is the side bonded to the core laminate. The drum side is always smoother than the matte side. For high frequency boards, sometimes the drum side of the foil is treated instead and bonded to the core. In this case it is known as reversed treated foil (RTF).
IPC-TM-650-2.2.17A defines the procedure for determining the roughness or profile of metallic foils used on PCBs. Profilometers are often used to quantify the roughness tooth profile of electro-deposited copper.
Nodule treated tooth profiles are typically reported in terms of 10-point mean roughness (Rz). Some manufacturers may also report root mean square (RMS) roughness (Rq). For standard foil this is the matte side. For RTF it is the drum side. Most often the untreated, or prepreg side, reports average roughness (Ra) in manufacturers’ data sheets.
With the realization of roughness having a detrimental effect on insertion loss (IL), copper suppliers began providing very low profile (VLP) and ultra-low profile (ULP) class of foils. VLP foils have treated roughness profiles less than 4 μm while ULP foils are less than 2 μm. Other names for ULP class are HVLP or eVLP, depending on the foil manufacturer.
It is important to obtain the actual vendor’s copper foil data sheet used by the respective laminate supplier for accurate modeling.
Oxide/Oxide Alternative Treatment
In order to promote good adhesion of copper to the prepreg material during the PCB lamination process, the copper surface is treated with chemicals to form a thin, nonconductive film of black or brown oxide. The controlled oxidation process increases the surface area, which provides a better bond between the prepreg and the copper surface. It also passivates the copper surface to protect it from contamination.
Although oxide treatment has been used for many years, eventually the industry learned that the lack of chemical resistance resulted in pink ring, which is indicative of poor adhesion between copper and prepreg. This weakness has led to oxide alternative (OA) treatments which rely on some sort of etching process, but no oxide layer is formed.
With the push for smoother copper to reduce conductor loss, newer chemical bond enhancement treatments, working at the molecular level, were developed to maintain copper smoothness, yet still provide good bonding to the prepreg.
Since OA treatment is applied to the drum side of the foil during the PCB Fabrication process, the OA roughness numbers should be used instead of Ra specified in foil manufacturer’s data sheets. RTF foil is modeled differently and discussed later in the case study.
Tale of Two Data Sheets
Everyone involved in the design and manufacture of PCBs knows the most important properties of the dielectric material are the dielectric constant (Dk) and dissipation factor (Df ).
Using Dk / Df numbers for stackup design and channel modeling from “Marketing” data sheets, like the example shown in Figure 3, will give inaccurate results. These data sheets are easily obtained when searching laminate supplier’s web sites.
Figure 3 Example of a “Marketing” data sheet easily obtained from laminate supplier’s web site. Source Isola Group.
Instead, real or “Engineering” data sheets, which are used by PCB fabricators to design stackups, should be used for PCB interconnect modeling. These data sheets define the actual thickness, resin content and glass style for different cores and prepregs. They include Dk / Df over a wide frequency range; usually from 100 MHz-10GHz.
Figure 4 Example of an “Engineering” data sheet showing Dk/Df for different glass styles and resin content over frequency. Source Isola Group.
Effective Dk Due to Roughness
Many engineers assume Dk published is the intrinsic property of the material. But in actual fact, it is the effective dielectric constant (Dkeff) generated by a specific test method. When simulations are compared against measurements, there is often a discrepancy in Dkeff, due to increased phase delay caused by surface roughness.
Dkeff is highly dependent on the test apparatus and conditions of how it is measured. One method commonly used by many laminate suppliers is the clamped stripline resonator test method, as described by IPC-TM-650, 2.5.5.5, Rev C, Test Methods Manual.
The measurements are done under stripline conditions using a carefully designed resonant element pattern card made with the same dielectric material to be tested. As shown in Figure 5, the card is sandwiched between two sheets of unclad dielectric material under test. Then the whole structure is clamped between two large plates; each lined with copper foil and are grounded. They act as reference planes for the stripline.
Figure 5 Illustration of clamped stripline resonator test method, as described by IPC-TM-650, 2.5.5.5, Rev C, Test Methods Manual
This method assures consistency of product when used in fabricated boards. It does not guarantee the values directly correspond to design applications.
This is a key point to keep in mind, and here is why.
Since the resonant element pattern card and material under test are not physically bonded together, there are small air gaps between the various layers that affect measured results. The small air gaps result in a lower Dkeff than what is measured in real applications using foil with different roughness bonded to the same core laminate. This is the primary reason for phase delay discrepancy between simulation and measurements.
If Dk and Rz roughness parameters from the manufacturers’ data sheets are known, then the effective Dk due to roughness (Dkeff_rough) of the fabricated core laminate can be estimated by [2]:
Equation 1
where: Hsmooth is the thickness of dielectric from data sheet; Rz is 10-point mean roughness from data sheet; Dk is dielectric constant from data sheet
Most EDA tools include a wideband causal dielectric model. To use it, you must enter Dk and Df at a particular frequency. I found it is usually best to use the values near the Nyquist frequency of the baud rate.
Modeling Copper Roughness
“All models are wrong but some are useful”– a famous quote by George E. P. Box, who was a British statistician in the mid-20th century. The same can be said when using various roughness models.
For example many roughness models require RMS roughness numbers, but often Rz is the only number available in data sheets, and vice versa. If Rz is defined as the sum of the average of the five highest peaks and the five lowest valleys of the roughness profile over a sample length, and Rq is the RMS value of that profile, then the roughness can be modeled as a triangular profile with a peak to valley height equal to Rz, as illustrated in Figure 6.
Figure 6 Triangular roughness profile model with peak to valley height equal to 10-point mean roughness Rz.
If we define the RMS height of the triangular roughness profile is equal to ∆, then:
Equation 2
And likewise, if we assume ∆ ~ Rq, then:
Equation 3
Several modeling methods were developed over the years to determine a roughness correction factor (KSR). When multiplicatively applied to the smooth conductor attenuation (αsmooth), the attenuation due to roughness (αrough) can be determined by:
Equation 4
Huray Model
In recent years, the Huray model has found its way into popular EDA software due to the continually increasing need for better modeling accuracy. The model is based on a non-uniform distribution of spherical shapes resembling “snowballs” and stacked together forming a pyramidal geometry.
By applying electromagnetic wave analysis, the superposition of the sphere losses can be used to determine the total loss of the structure. Since the losses are proportional to the surface area of the roughness profile, an accurate estimation of a roughness correction factor (KSRH) can be analytically solved by [4]:
Equation 5
Although it has been proven to be a pretty accurate model, it relied on analysis of scanning electron microscopy (SEM) pictures of the treated surface and tuning of parameters for best fit to measured data. This is not a practical solution if all you have is roughness parameters from manufacturers’ data sheets.
Simonovich “Cannonball” Conductor Roughness Model (A.K.A. Cannonball-Huray Model)
Building upon the work already done by Huray, and using the Cannonball stack principle, the sphere radius and flat base area parameters are easily estimated solely from roughness parameters published in manufacturers’ data sheets.
As illustrated in Figure 7 there are three rows of equal sized spheres stacked on a square tile base. Nine spheres are on the first row, four spheres in the middle row, and one sphere on top. This stacking arrangement is known as close-packing of equal spheres, but more commonly known as the “Cannonball” stack due to the method used by sailors to stack actual cannonballs aboard ships.
Figure 7 Cannonball-Huray physical model. The height of the stack is the RMS height of the peak to valley profile equal to Rz from data sheets.
If we could peer into the stack and imagine a pyramid lattice structure connecting to the center of all the spheres, then the total height is equal the height of two pyramids plus the diameter of one sphere.
Given the height of the Cannonball stack (∆) is equal to the RMS value of the peak to valley roughness profile; then from method described in my earlier papers, determining the sphere radius (r ), from Rz found in data sheets, can be further simplified and approximated as [13]:
and base area (Aflat) as:
Equation 7
Because the model assumes the ratio of Amatte/Aflat = 1, and there are only 14 spheres, the original Cannonball-Huray model can be further simplified to:
Equation 8
where: KCH (f) = Cannonball-Huray roughness correction factor, as a function of frequency; δ (f) = skin-depth, as a function of frequency in meters; r = the radius of spheres in meters (Equation 6)
CMP28 Case Study Revisited
To test the accuracy of the model, stackup details and measured data from a CMP28 test platform, design kit, courtesy of Wildriver Technology, shown in Figure 8, was used for model validation. The PCB stackup is shown in Figure 9
Two different sets of S-parameter (s2p) files from a 2 inch and 8 inch single-ended (SE) stripline traces shown were used in this study. The original set of measurements, from my previous papers, and a second set provided as part of CMP-28 design kit from another PCB were used for model correlation.
The 6 inch transmission line segment S-parameter data was de-embedded using Ataitec ISD software [8] for both sets of data.
Figure 8 Photo of a portion of CMP-28 test platform courtesy of Wildriver Technology used for model validation.
Figure 9 CMP-28 PCB Stackup
The PCB was fabricated with Isola FR408HR 3313 core and prepreg, with 1 oz. RTF. Dk and Df at 10GHz were obtained from the FR408HR data sheet found on their web site and shown in Figure 10 & Figure 11.
Figure 10 Isola FR408HR data sheet used for core dielectric properties.
Figure 11 Isola FR408HR data sheet used for prepreg dielectric properties.
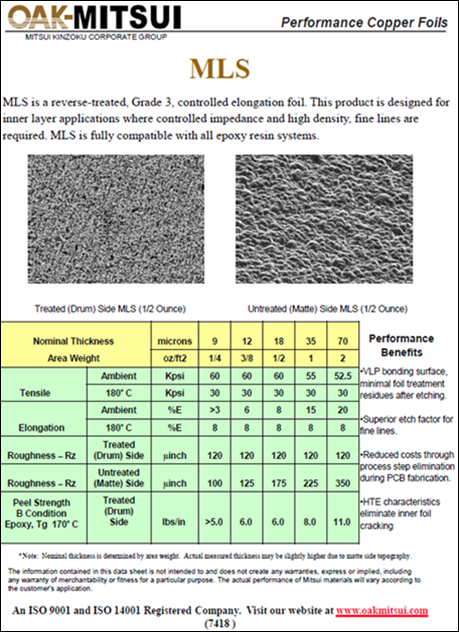
The foil used on FR408HR core laminates is MLS, Grade 3, controlled elongation RTF from Oak-matsui. Roughness Rz parameters for drum and matte sides are 120μin (3.048 μm) and 225μin (5.715μm) respectively for 1 oz. copper foil.
Figure 12 MLS RTF foil data sheet used on FR408HR laminate.
An oxide or oxide alternative (OA) treatment is usually applied to the copper surfaces prior to final PCB lamination. When it is applied to the matte side of RTF, it tends to smoothen the macro-roughness slightly. At the same time, it creates a surface full of microvoids which follows the underlying rough profile and allows the resin to fill in the cavities, providing a good anchor.
MultiBond MP from Macdermid Enthone is an example of an oxide alternative micro-etch treatment commonly used in the industry. Typically 50 μin (1.27μm) of copper is removed when the treatment is completed, depending on the board shop’s process control, as per Figure 13.
In a subsequent paper by J.A. Marshall, presented at IPC APEX 2015 titled, “Measuring Copper Surface Roughness for High Speed Applications” [11], there is data supporting the hypothesis that RTF roughness gets smoother after OA application.
Figure 13 Macdermid Enthone MultiBond MP data sheet reference from their web site.
Table 1 summarizes the PCB design parameters, dielectric material properties and copper roughness parameters obtained from respective manufactures’ data sheets.
Table 1 CMP-28 Test Board and Data Sheet Parameters
| Parameter | FR408HR/RTF |
| Dk Core/Prepreg | 3.65/3.59 @10GHz |
| Df Core/Prepreg | 0.0094/0.0095 @ 10GHz |
| Rz Drum side | 3.048 μm |
| Rz Matte side before Micro-etch | 5.715 μm |
| Rz Matte side after Micro-etch | 4.445 μm |
| Trace Thickness, t | 1.25 mil (31.7μm ) |
| Trace Etch Factor | 60 deg |
| Trace Width, w | 11 mils (279.20 μm) |
| Core thickness, H1 | 12 mils (304.60 μm) |
| Prepreg thickness, H2 | 10.6 mils (269.00 μm) |
| GMS trace length | 6 in (15.23 cm) |
From Table 1 and by applying Equation 1, Dkeff of core and prepreg due to roughness were determined to be:
Next, the Cannonball model’s sphere radiuses, for matte and drum side of the foil, were determined to be:
Because most EDA tools only allow a single value for the radius parameter, the average radius (ravg) was determined to be:
Equation 9
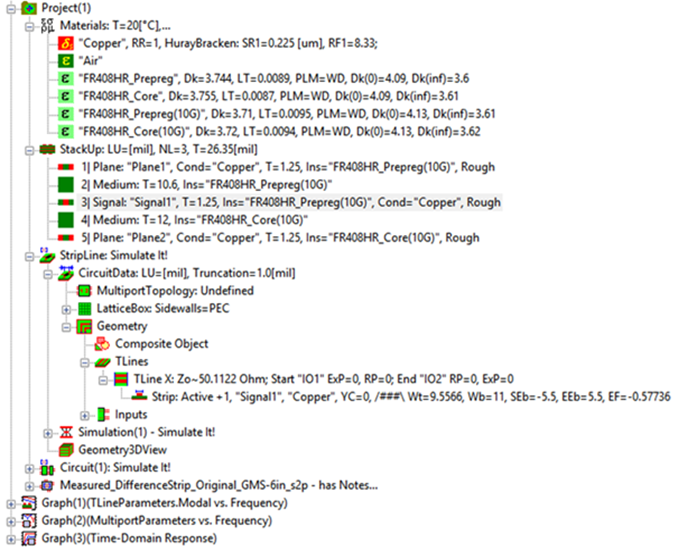
Simbeor electromagnetic software from Simberian Inc. [10] was used for modeling the transmission lines. It includes the latest and greatest dielectric and conductor roughness models, including the Huray-Bracken causal metal model.
Solution explorer pane and solution tree, as shown in Figure 14, allows you to edit and view solution data as a tree structure. All parameters from Table 1 were entered here.
Simbeor requires two parameters; roughness factor (RF1) and sphere radius (SR1). Because the Cannonball model always has N=14 spheres and base area (Aflat) is always 36r2, r2 cancels out and RF1 can be simplified to:
Equation 10
Sphere radius (SR1) is ravg = 0.225 as calculated from Equation 9.
Figure 14 Simbeor Solution Explorer Pane and Solution Tree
The wideband causal dielectric model option was used to model dielectric properties over frequency. Effective Dk due to roughness for core and prepreg, calculated above, were substituted instead of data sheet values. Standard copper resistivity of 1.724e-8 ohm-meter was used.
After the transmission lines were modeled and simulated, the S-parameter results were saved in touchstone format. Keysight ADS [5] was used for further simulation analysis and comparison.
Dkeff can be derived from phase delay. This is also known as time delay (TD) and is often used as a metric for simulation correlation accuracy for phase. TD, as a function of frequency, in seconds, is calculated from the unwrapped measured transmission phase angle, and is given by:
Equation 11
and:
Dkeff , as a function of frequency, is then given by:
Equation 12
where:c = speed of light (m/s); Length = length of conductor (m)
Figure 15 compares the simulated results vs measurement of a 6inch, de-embedded stripline trace. The red plots are measured from CMP-28 design kit data. The data was bandwidth limited to 35 GHz. The blue plots are the original measured data used in my previous paper [5]. The green plots are modeled with data sheet values only with oxide alternative treatment applied. SE IL is shown on the left and Dkeff is shown on the right. As can be seen, there is excellent correlation.
Figure 15 Measured vs simulated insertion loss (left) and Dkeff (right) with OA etch treatment applied.
The author of [1] suggests is that because I had the measured data, Rz was “adjusted” to show excellent results. What he is implying is my “adjusting” the roughness, due to the oxide treatment, was the reason for such good results, in spite of the fact Macdermid’s OA data sheet reports typical 50 μin of copper removal after treatment and data from [11] showing RTF gets slightly smoother after OA treatment.
So ok, let’s see what happens if I didn’t adjust the roughness due to OA treatment. Instead of using Rz matte side after micro-etch (4.445 μm ) roughness, we will use 5.715 μm from data sheet.
This will affect Dkeff of prepreg and average sphere radius ravg , so we will recalculate them:
And average radius is:
Figure 16 compares the simulated results vs measurement. The red plots are measured from CMP-28 design kit data. The blue plots are the original measured data used in my previous paper [5]. The green plots are modeled with data sheet values only without oxide alternative treatment applied. SE IL is shown on the left and Dkeff is shown on the right.
As can be seen, there is still excellent correlation with insertion loss even though OA was not considered. As expected using the rougher number would increase effective Dk. But in the end the TDR plots in Figure 17shows impedance change is negligible.
Figure 16 Measured vs simulated insertion loss (left) and phase delay (right) without OA etch treatment applied.
Figure 17 Measured vs simulated TDR plots with OA etch treatment (left) and without (right).
Summary and Conclusions
By using Cannonball-Huray model, with copper foil roughness and dielectric material properties obtained solely from respective manufacturers’ data sheets, practical PCB interconnect modeling for high-speed design is now achievable using commercial field-solving software employing Huray model.
Measured results from two different boards confirmed there are variations due to manufacturing that would affect material model extraction method accuracy.
When oxide alternative treatment was not considered, even though the matte side roughness of RTF gets smoothened during the PCB fabrication process, the simulated results still show excellent correlation to the original measured data from previous paper [5].
References
[1] Y. Slepnev, “Conductor surface roughness modeling: From “snowballs” to “cannonballs”.
[2] B. Simonovich, “A Practical Method to Model Effective Permittivity and Phase Delay Due to Conductor Surface Roughness”. DesignCon 2017, Proceedings, Santa Clara, CA, 2017
[3] L. Simonovich, “Practical method for modeling conductor roughness using cubic close-packing of equal spheres,” 2016 IEEE International Symposium on Electromagnetic Compatibility (EMC), Ottawa, ON, 2016, pp. 917-920. doi: 10.1109/ISEMC.2016.7571773.
[4] Huray, P. G. (2009) “The Foundations of Signal Integrity”, John Wiley & Sons, Inc., Hoboken, NJ, USA., 2009
[5] L.Simonovich, “Practical Model of Conductor Surface Roughness Using Cubic Close-packing of Equal Spheres”, EDICon 2016, Boston, MA
[6] Keysight Advanced Design System (ADS) [computer software], (Version 2017). URL: http://www.keysight.com/en/pc-1297113/advanced-design-system-ads?cc=US&lc=eng.
[7] Isola Group S.a.r.l., 3100 West Ray Road, Suite 301, Chandler, AZ 85226. URL: http://www.isola-group.com/
[8] Ataitec, URL: http://ataitec.com/products/isd/
[9] V. Dmitriev-Zdorov, B. Simonovich, I. Kochikov, “A Causal Conductor Roughness Model and its Effect on Transmission Line Characteristics”, DesignCon 2018 Proceedings, Santa Clara, CA, 2018
[10] Simberian Inc., 2629 Townsgate Rd., Suite 235, Westlake Village, CA 91361, USA, URL: http://www.simberian.com/
[11] John A. Marshall, “Measuring Copper Surface Roughness for High Speed Applications”, IPC APEX Expo 2015.
[12] Macdermid Enthone, Multibond MP, Inner Layer Oxide Alternative Bonding. URL: https://electronics.macdermidenthone.com/products-and-applications/printed-circuit-board/surface-treatments/innerlayer-bonding
[13] B. Simonovich, “PCB Interconnect Modeling Demystified”. DesignCon 2019, Proceedings, Santa Clara, CA, 2019.
[14] Wild River Technology LLC 8311 SW Charlotte Drive Beaverton, OR 97007. URL: https://wildrivertech.com/